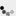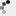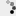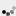Математическая энциклопедия - кутта - мерсона метод

пятиэтапный метод Рунге Кутта 4-го порядка точности. Применительно к задаче Коши

метод имеет вид:

Величина служит для оценки погрешности метода и для автоматического выбора шага интегрирования. Если е предписанная точность вычислений, то шаг интегрирования выбирается следующим образом. Берется нек-рый начальный шаг и производятся вычисления по формулам (2). Вычисляется величина R. При шаг интегрирования уменьшается в два раза. При . шаг увеличивается вдвое. Если же то шаг считается выбранным правильно. После этого в качестве начальной точки х 0 берется точка х п+h и весь процесс повторяется снова. В качестве приближенного решения выступает величина у ². Величина y¹ носит вспомогательный характер. В связи с тем, что

то ость формула для вычисления у ¹ является как бы "вложенной" в формулу для вычисления у ², описанный выше метод оценки погрешности и выбора шага интегрирования наз. методом вложенных форм. Имеются стандартные программы К.М. м. на языке алгол [1], [2].

Лит.:[1] С h r i s t i a n s e n J., "Numer. Mach.", 1970, Bd 14, S. 317-24; [2] L u k e h a r t P. M., "Communs Assoc. Comput. Math.", 1963, v. 6, № 12, p. 737-38; [3] Fox L., Numerical solution of ordinary and partial differential equations, Oxf., 1962; [4] Lance G. N., Numerical methods for high speed computers, L., 1960. В. В. Поспелов.

Математическая энциклопедия. — М.: Советская энциклопедия

И. М. Виноградов

1977—1985